INTRODUCTION
Never in history have more people had access to advanced encryption in their homes, offices, and pockets than we do now. The most basic online transactions and communications that Internet users conduct every day are thoroughly encrypted in transit, and are undecipherable without proper keys.
The democratization of encryption is a recent phenomenon: only since the 1990s has computer encryption been open and freely available. But humans have been communicating with codes and ciphers for thousands of years, using rudimentary encryption methods to protect trade secrets and military orders, or simply to keep information private from prying eyes.
Before Computers
The technology that keeps your text messages private started on the banks of the Tigris River, 3500 years ago.
One of the first traces is one very well written-up and documented cuneiform tablet in Mesopotamia, found around 1500 B.C. It was an encrypted message in which craftsmen camouflaged the recipe for a pottery glaze that was a highly coveted item at the time. As it turned out, once the secret had been unearthed and discovered, recipes were no longer encrypted because just about everyone knew it.
The recipe was encrypted through a relatively simple substitution method: one cuneiform symbol was used for another. That way, basically, the message got garbled.
Another early example is the Atbash system, which predates the birth of Christ. It is also a simple replacement of the last letter in the alphabet with the first letter, the second-to-last with the second – a simple transposition of letters which was good enough, and was even used in the Bible, through the Hebrew ciphers.
In the Kama Sutra, in India, around the 4th century, there are references in the 44th and 45th chapters that men and women should practice cryptography. The Kama Sutra deals with all sorts of intercommunication between men and women and could obviously also entail secret communication. That communication, where men and women should have a language of their own, was intended so that neighbors would not understand.
Early cryptology began with the spread of a new religion and the Arab conquest, for five major reasons. Very early on, the Arab World had to rely on translations; it also had to study its own language. There were well-known advances in mathematics. There was a need for effective administration in the Arab Muslim state, a realm that kept on spreading.
Already in the early 800s, fundamental tenets like statistical techniques were developed, which took the West centuries to develop. When frequency analysis was discovered in the West, the Mesopotamian mathematician and philosopher “Al-Kindi” had already done it, in the 850s or 860s. He came up with substitution ciphers, the transposition ciphers, methods that the West applied around 600 years later.
The real necessity for a development of cryptological means begins with diplomatic communication and rivalry between states. In Europe it begins in Italy, where there is a plethora of city-states, and communication between these individual units needed to develop along certain secret lines. So, in the 13th and 14th centuries, Italian city-states and the Vatican began developing their own systems, simply because their reliance on plain messages didn’t work anymore.
This, in turn, led to the official need for such a system for the Papal court, and the Italian Leon Battista Alberti was asked to develop a usable system. In around 1450, he invented a famous cipher disk. This is the first very important invention in Western cryptography.
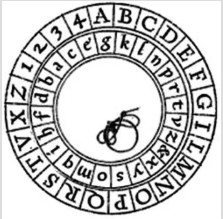
The cryptographer monk Trithemius developed the disk into a 24-letter square. The square does the same thing that the cipher disk accomplishes – however, it has one very nice advantage:
A soldier in the field has a hard time cutting out two concentric paper disks and labelling them, while it is easy for anyone to write 24 letters, write them horizontally and vertically, and shift them by one letter each line. That is a very practical application for someone in the field to write his own square, and have a powerful cryptographic tool.
Some early cryptographer work was sometimes compared to magic – and Trithemius was accused of wielding “black magic.”
He devised a cryptographic system in his Steganographia, and before he’d even finished it – he never finished it – he informed a fellow monk of what he was going to do, and that fellow monk totally misinterpreted the letter and accused him of black magic, which got him into a lot of trouble. The Steganographia wasn’t published until 110 years, or so, later.
On the commercial side, the Duke of Wolfenbüttel’s son was camouflaging an encrypted message by simply listing the pounds and tons of wheat that a merchant might ship from point A to point B.
In other words, it says, “I herewith send you an invoice for 17 pounds of barley and 22 pounds of wheat,” or whatever it was. Of course, the numbers are the encrypted message, which means your partner has to be able to decode these numbers, which means they both have to have a codebook. For example, number 17 means “The Duke of Windsor,” and number 22 means “the Queen of England.”
Another early user of code was the Count of Vergennes, who in the 18th-century France applied coded messages into travel visas. The Count of Vergennes, the French foreign minister, informed all his consular officials abroad that anyone applying for, “a passport” had to submit himself or herself to public scrutiny, and was investigated. They either volunteered information, innocently enough, or employees in the embassy would go around and collect information on that person.
The person was analyzed as to physical features, like: Is he bald? Is he cross-eyed? Is he tall? Is he short? Does he have a pot-belly? Those are outward and simple features that any official could jot down when the person presented himself. But, beyond that, there was: Is he married? Is he a good lover? Does he have a mistress? And what is his purpose for applying for a passport? To visit relatives? He wants to meet craftsmen, he wants to engage in commerce in Paris?
Beyond that, the embassy official also had to pass judgment on his psyche. Is he depressed? Is he an alcoholic? Does he look like an alcoholic? Is he friendly, is he outgoing? And all of that would they be translated into what you could call a relatively large calling card with his name, asking to see the Count of Vergennes.
That calling card was embellished with a beautiful frame, and the frame carried a code. If it had a sunflower, it meant the man was friendly, and if it had a moon instead of the sunflower, then he was an aggressive type. When it carried 12 little circles, he was very wealthy. When it only carried 4 circles, then he was of average means. When it didn’t carry a single circle, he was poor. And so on.
Initially each of these embassy offices had to have an engraver who would personalize this card. When Vergennes realized that you had to have a whole legion of engravers sworn to secrecy, his next step was to have his own little printing press, and print this information, but now in numerical form. You now had, simply, lots of numbers, and they all had their meaning.
It started out in the upper-left corner with an N. If the N was tall, the man was tall; if the n was small, the man was short. If it had a circle behind it, it means he was married. And then came the numbers. So, of course, the person who had this card thought, “Aha, I am number 17,222.” In reality, of course, this was all encoded.
The irony was that this card was given to the traveler. It wasn’t given to him in a sealed envelope. He could see it and it was supposedly perfectly innocent. He was then to go to Paris and present himself to the Count of Vergennes, and the Count of Vergennes would probably spend two minutes with him, but would immediately turn around and either analyze the card or have someone on his staff analyze it, and if necessary, send a policeman after him, depending on the type of business or information that was available.
If you had a wealthy merchant, then they would try to delay his return to his home country, because the longer such a wealthy person would stay in Paris, the more money he would spend. If the gentleman had a police record back home, then that was an indication to really keep an eye on him.
You don’t normally entrust the messenger with the message and the system was so refined that after the French Revolution, it continued to be used into the 19th Century.
So, you have cryptology and you have steganography, which is a system where you cannot detect a message. If I send you an encrypted message, and you can’t decipher it, you can tear it up. But steganographic communication means, at face value, visually, it looks perfectly innocent. Nonetheless, embedded in it, is a secret message.
Although cryptography has a long and complex history, it wasn’t until the 19th century that it developed anything more than ad hoc approaches to either encryption. Edgar Allan Poe used systematic methods to solve ciphers in the 1840s. In particular he placed a notice of his abilities in a Philadelphia paper, inviting submissions of ciphers, of which he proceeded to solve almost all. He later wrote an essay on methods of cryptography which proved useful as an introduction for novice British crypto analysts attempting to break German codes and ciphers during World War I.
Cryptography, and its misuse, were involved in the execution of Mata Hari and in Dreyfus’ conviction and imprisonment, both in the early 20th century. In World War I the Admiralty’s Room 40 broke German naval codes and played an important role in several naval engagements during the war, notably in detecting major German sorties into the North Sea that led to the battles of Dogger Bank and Jutland as the British fleet was sent out to intercept them.
However its most important contribution was probably in decrypting the Zimmermann Telegram, a cable from the German Foreign Office sent via Washington to its ambassador Heinrich von Eckardt in Mexico which played a major part in bringing the United States into the war.
In 1917, Gilbert Vernam proposed a teleprinter cipher in which a previously prepared key, kept on paper tape, is combined character by character with the plaintext message to produce the ciphertext. This led to the development of electromechanical devices as cipher machines, and to the only unbreakable cipher, the one time pad.
During the 1920s, Polish naval-officers assisted the Japanese military with code and cipher development. Mathematical methods proliferated in the period prior to World War II
By World War II, mechanical and electromechanical cipher machines were in wide use, although manual systems continued in use. Great advances were made in both cipher design and cryptanalysis, all in secrecy.
Information about this period has begun to be declassified as the official British 50-year secrecy period has come to an end. US archives have slowly opened and assorted memoirs and articles have appeared.
The Germans made heavy use, in several variants, of an electro-mechanical rotor machine known as Enigma. Mathematician Marian Rejewski, at Poland’s Cipher Bureau, deduced the detailed structure of the German Army Enigma in December 1932, using mathematics and limited documentation. Rejewski and his mathematical Cipher Bureau colleagues, Jerzy Różycki and Henryk Zygalski, continued reading Enigma and keeping pace with the evolution of the German Army machine’s components and encipherment procedures. The Cipher Bureau initiated French and British intelligence representatives into the secrets of Enigma decryption when the WW2 broke out.
German code breaking in World War II also had some success, most importantly by breaking the Naval Cypher No. 3. This enabled them to track and sink Atlantic convoys. It was only Ultra intelligence that finally persuaded the admiralty to change their codes in June 1943.
At the end of the War, on 19 April 1945, Britain’s top military officers were told that they could never reveal that the German Enigma cipher had been broken because it would give the defeated enemy the chance to say they “were not well and fairly beaten”.
US Navy cryptographers (with cooperation from British and Dutch cryptographers after 1940) broke into several Japanese Navy crypto systems. The break into one of them, JN-25, famously led to the US victory in the Battle of Midway; and to the publication of that fact in the Chicago Tribune shortly after the battle, though the Japanese seem not to have noticed, because they kept using the JN-25 system. A US Army group, the SIS, managed to break the highest security Japanese diplomatic cipher system even before the World War II began.
Allied cipher machines used in World War II included the British TypeX and the American SIGABA; both were electromechanical rotor designs similar in spirit to the Enigma, albeit with major improvements. Neither is known to have been broken by anyone during the War.
MODERN CRYPTOGRAPHY
Encryption in modern times is achieved by using mathematical algorithms that have a unique key to encrypt and decrypt information. These keys convert the messages and data into “digital gibberish” through encryption and then return them to the original form through decryption.
In general, the longer the key – the longer it takes to crack the code by brute force, i.e. the attacker has to try every possible key. To put this in context, each binary unit of information, or bit, has a value of 0 or 1. An 8-bit key would then have 256 or 2^8 possible keys. A 56-bit key would have 2^56, or 72 quadrillion, possible keys to try and decipher the message.
However, as technology advances, so does the quality of encryption. Since World War II, one of the most notable advances in the study of cryptography is the introduction of the asymmetric key cyphers (sometimes termed public-key cyphers). These are algorithms which use two mathematically related keys for encryption of the same message. Some of these algorithms permit publication of one of the keys, due to it being extremely difficult to determine one key simply from knowledge of the other.
Beginning around 1990, the use of the Internet for commercial purposes and the introduction of commercial transactions over the Internet called for a widespread standard for encryption. In the beginning, the most commonly used algoritm was the Data Encryption Standard (DES). This has been replaced by the AES after public competition organized by NIST.
In the late 1990s to early 2000s, the use of public-key algorithms became a more common approach for encryption, and soon a hybrid of the two schemes became the most accepted way for e-commerce operations to proceed. Additionally, the creation of a new protocol known as the Secure Socket Layer, or SSL, led the way for online transactions to take place. Transactions ranging from purchasing goods to online bill pay and banking use SSL. Furthermore, as wireless Internet connections became more common among households, the need for encryption grew, as a level of security was needed in these everyday situations.
Claude Shannon
Claude E. Shannon is considered by many to be the father of mathematical cryptography. Shannon worked for several years at Bell Labs, and during his time there, he produced an article titled “A mathematical theory of cryptography”. This article was written in 1945 and eventually was published in the Bell System Technical Journal in 1949.
It is commonly accepted that this paper was the starting point for the development of modern cryptography.
Shannon identified the two main goals of cryptography: secrecy and authenticity.
In his works, Shannon described the two basic types of systems for secrecy. The first are those designed with the intent to protect against hackers and attackers who have infinite resources with which to decode a message (theoretical secrecy), and the second are those designed to protect against hackers and attacks with finite resources with which to decode a message (practical, or computational security).
Most of Shannon’s work focused around theoretical secrecy and introduced a definition for the “unbreakability” of a cipher. Shannon determined that this could only be obtained with a secret key, whose length given in binary digits, was greater than or equal to the number of bits contained in the information being encrypted.
Shannon’s work influenced further cryptography research in the 1970s, as the public-key cryptography developers, M. E. Hellman and W. Diffie cited Shannon’s research as a major influence. His work also impacted modern designs of secret-key ciphers. At the end of Shannon’s work with cryptography, progress slowed until Hellman and Diffie introduced their paper involving “public-key cryptography”.
An encryption standard
The mid-1970s saw two major advances. First was the publication of the draft Data Encryption Standard in the U.S. in 1975. The proposed DES cipher was submitted by a research group at IBM, at the invitation of the National Bureau of Standards (now NIST), in an effort to develop secure electronic communication facilities for businesses, such as banks and other large financial organizations. After advice and modification by the NSA it was adopted and published as a Federal Information Processing Standard Publication in 1977. DES was the first publicly accessible cipher to be ‘blessed’ by a national agency such as the NSA. The release of its specification by NBS stimulated an explosion of public and academic interest in cryptography.
The aging DES was officially replaced by the Advanced Encryption Standard (AES) in 2001. After an open competition, NIST selected an entry submitted by two Belgian cryptographers, to be the AES.
Most Full Disk Encryption solutions available today, rely on 256-bit AES for the encryption of data. Additionally, each sector of the disk has a unique key, which is normally created as a result of the output of the previously encrypted sector in a one-way key chain. This makes FDE extremely resilient to brute force attacks as the attacker has to start again on the next sector – and he does not know if he is hacking on a sector containing information – or not.
Public key
The second development, in 1976, was perhaps even more important, because it fundamentally changed the way crypto systems would work. This was the publication of the paper “New Directions in Cryptography” by Whitfield Diffie and Martin Hellman. It introduced a radically new method of distributing cryptographic keys, which went far toward solving one of the fundamental problems of cryptography, key distribution, and has become known as Diffie-Hellman key exchange. The article also stimulated the almost immediate public development of a new class of enciphering algorithms, the asymmetric key algorithms.
Prior to that time, all useful modern encryption algorithms had been symmetric key algorithms, in which the same cryptographic key is used with the underlying algorithm by both the sender and the recipient, who must both keep it secret. All of the electromechanical machines used in World War II were of this logical class, as were the Caesar and Atbash ciphers and essentially all cipher systems throughout history. The ‘key’ for a code is, of course, the codebook, which must likewise be distributed and kept secret, and so shares most of the same problems in practice.
Of necessity, the key in every such system had to be shared between the communicating parties in some secure way before the encryption can be used. This can be a courier with a briefcase handcuffed to a wrist, or face-to-face contact, or a loyal carrier pigeon. This requirement is never trivial and very rapidly becomes unmanageable as the number of participants increases, or when secure channels aren’t available for key exchange, or when, as is sensible cryptographic practice, keys are frequently changed. In particular, if messages are meant to be secure from other users, a separate key is required for each possible pair of users. A system of this kind is known as a secret key, or symmetric key cryptosystem.
In contrast, asymmetric key encryption uses a pair of mathematically related keys, each of which decrypts the encryption performed using the other. Most of these algorithms also have the additional property that one of the paired keys cannot be deduced from the other by any known method other than trial and error.
An algorithm of this kind is known as a public key or asymmetric key system.
Using such an algorithm, only one key pair is needed per user. By designating one key of the pair as private (always secret), and the other as public (often widely available), no secure channel is needed for key exchange. So long as the private key stays secret, the public key can be widely known for a very long time without compromising security, making it safe to reuse the same key pair indefinitely.
For two users of an asymmetric key algorithm to communicate securely over an insecure channel, each user will need to know their own public and private keys as well as the other user’s public key.
At the start of a message, you start by exchanging public keys, unencrypted over an insecure line. Person 1 then encrypts a message using her private key, and then re-encrypts that result using person 2’s public key. The double-encrypted message is then sent as digital data over a wire. Person 2 receives the data and decrypts it using his own private key, and then decrypts what’s “inside” using person 1’s public key. If the final result is recognizable as a message, you can be confident that the message actually came from someone who knows person 1’s private key, and that anyone eavesdropping on the channel will need the receiver’s private key in order to understand the message.
Asymmetric algorithms is what mathematics call one-way functions, which require relatively little computational power to execute, but vast amounts of power to reverse, if reversal is possible at all.
A classic example of a one-way function is mixing blue and yellow colour to a green shade. Unless you know how much yellow (or blue) that was used to get the green shade – you have an infinite amount of possibilities.
Since symmetric algorithms can often use any sequence of bits as a key, a disposable session key can be quickly generated for short-term use. Consequently, it is common practice to use a long asymmetric key to exchange a disposable, much shorter (but just as strong) symmetric key. The slower asymmetric algorithm securely sends a symmetric session key, and the faster symmetric algorithm takes over for the remainder of the message.
Asymmetric key cryptography, Diffie-Hellman key exchange, is the best known of the public key/private key algorithms.
Hashing
Hashing is a common technique used in cryptography to encode information quickly using typical algorithms. Generally, an algorithm is applied to a string of text, and the resulting string becomes the “hash value”. This creates a “digital fingerprint” of the message, as the specific hash value is used to identify a specific message. The output from the algorithm is also referred to as a “check sum”. Hashing is good for determining if information has been changed. If anything changes in the message the checksum is also changed.
It is important to note that hashing is not the same as encrypting, only the integrity of the message can be measured with hashing.
Hash functions can be used to verify digital signatures, so that when signing documents via the Internet, the signature is applied to one particular individual. Much like a hand-written signature, these signatures are verified by assigning their exact hash code to a person. Furthermore, hashing is applied to passwords for computer systems. A user on the system would first create a password. That password would be hashed, using an algorithm or key, and then stored in a password file. This is still prominent today, as web applications that require passwords will often hash user’s passwords and store them in a database.
Cryptography politics
The public developments of the 1970s broke the near monopoly on high quality cryptography held by government organizations. For the first time ever, those outside government organizations had access to cryptography not readily breakable by anyone.
Considerable controversy, and conflict, both public and private, began more or less immediately. In many countries, export of cryptography is subject to restrictions. Until 1996 export from the U.S. of cryptography using keys longer than 40 bits was sharply limited.
One of the most significant people favoring strong encryption for public use was Phil Zimmermann. He wrote and then in 1991 released PGP (Pretty Good Privacy), a very high quality crypto system. He distributed a freeware version of PGP when he felt threatened by legislation that would require backdoors to be included in all cryptographic products developed within the US. His system was released worldwide shortly after he released it in the US, and that began a long criminal investigation of him by the US Government Justice Department for the alleged violation of export restrictions. The Justice Department eventually dropped its case against Zimmermann, and the freeware distribution of PGP has continued around the world.
Modern cryptanalysis
While modern ciphers like AES and the higher quality asymmetric ciphers are widely considered unbreakable, poor designs and implementations are still sometimes adopted and there have been important cryptanalytic breaks of deployed crypto systems in recent years.
Notable examples of broken crypto designs include the first Wi-Fi encryption scheme WEP, the Content Scrambling System used for encrypting and controlling DVD use, the A5/1 and A5/2 ciphers used in GSM cell phones.
All of these are symmetric ciphers. Thus far, not one of the mathematical ideas underlying public key cryptography has been proven to be ‘unbreakable’, and so some future mathematical analysis advance might render systems relying on them insecure. While few informed observers foresee such a breakthrough, the key size recommended for security as best practice keeps increasing as increased computing power required for breaking codes becomes cheaper and more available.
